BSP-Net
参考论文
BSP-Net: Generating Compact Meshes via Binary Space Partitioning
Introduction
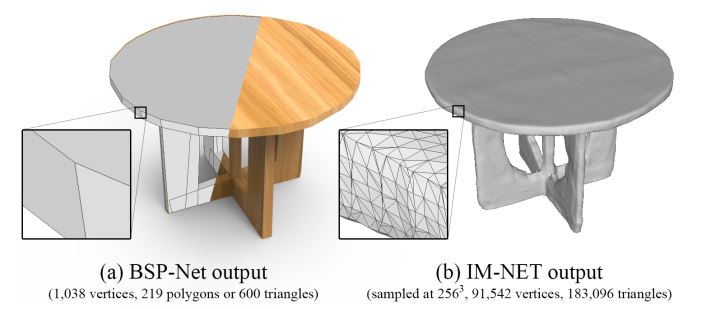
对于通过implicit function,利用等值曲面提取生成mesh的方法具有计算代价高,不能生成尖锐几何特征的缺点。利用BSP不断地将空间递归分割为凸面体的集合,论文提出了BSP-Net,通过对凸多面体的分解来表示三维模型。对于三维模型的重建则利用BSP-Net建立的BSP Tree中凸多面体的集合。利用凸多面体来表示三维模型,具有占用空间小(compact)以及能够表示尖锐几何特征的特点,且不受拓扑结构的限制。除此之外,BSP-Net是无监督的。
Background
Bianry Space Partitioning(BSP-Tree)
概念
BSP树是一种数据的组合形式,构建的过程从某种类型的数据开始,将其分成两个部分,再将这两个部分继续分割,直到得到最小的单元。
BSP Tree in Computer Graphics
BSP Tree起初用于加快渲染器的渲染速度:
当渲染器去渲染一个场景时,每一个多边形的位置以及面的朝向影响了最终的渲染效果,渲染器需要清楚每个多边形在当前视角下是否可见以及光线等信息。在拥有海量多边形的物体上,对每个物体进行上述处理无疑需要消耗大量的时间。因此,渲染器会将多边形分组,这些分组就是BSP Tree的分支。算法会遍历BSP Tree去找到具有相似特征的多边形,并将它们归为一个组,而不是单独对每个多边形进行处理。
下图展示了BSP Tree对一个立方体的分割,其中最小的单元为立方体mesh的每一个面:
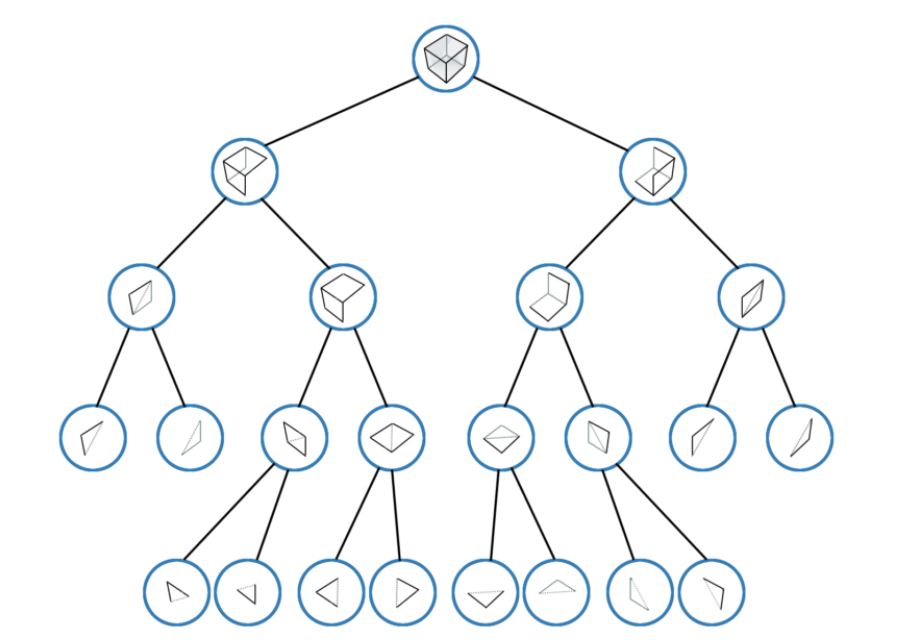
这篇论文中的BSP-Tree与原始的概念并不完全相同,论文中的BSP-Tree并非二叉树,而是n叉树,其中B(Binary)代表平面将空间切分成两个部分。
Construct Solid Geometry(CSG)
CSG是通过一组基元以及布尔运算来表示一个物体的方法,运算包括求并集、交集以及相减等。在这片论文中,在获得了凸多面体集合后,采用并集的方式得到显式的多面体网格模型。
Method
BSP-Net学习了一个Implicit field,给定n个点的坐标,网络输出对应的值表示该点是否位于模型内。
对于Implicit fuction的组合以构成最终的模型,可分为三步:
-
一个含有p个平面等式的集合P,每个平面将空间分割成了两个部分。
-
矩阵将上一步中的平面进行聚合,得到c个凸多面体作为三维模型的基元(primitives)/部分(parts)。
-
最后,通过对上述基元的组合,得到单一的表示输出模型的implicit field。
以二维空间为例,BSP-Tree的结构如下图所示,最上层为二维空间中的线,将空间分为两个部分,之后通过线的组合得到几何形状的集合,最后再将这些几何形状组合到一起,得到最终的输出:
Archetecture of BSP-Net
BSP-Net的网络结构如下图所示:
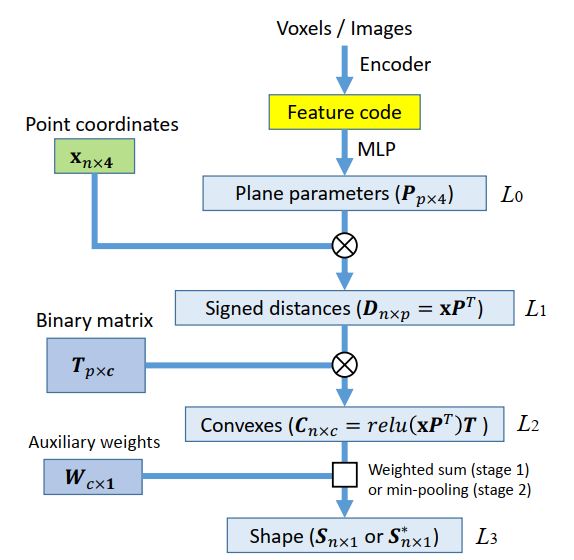
Layer 1: hyperplane extraction
通过编码器得到的feature code经过MLP得到矩阵用于表示平面集合中平面的参数,其中p为平面的个数,参数对应的平面等式为;之后,取样的n个点的坐标与相乘,得到符号距离,则对于其中一个点x的第i个符号距离,如果距离为负,则点位于第i个平面内,否则,位于第i个平面外。
Layer 2: hyperplane grouping
为二值矩阵,用于选取平面将其组合为c个凸多面体,输出为矩阵表示凸多面体集合,在网络中,采用加和的方式将选定的平面聚合在一起:
Layer 3: shape assembly
通过求和以及min-pooling将凸多面体聚合起来,得到最终三维模型的Implicit function。
其中,为权重矩阵, ,表示对区间的切分。上述公式中,仅是对点是否位于模型内的一种估计,存在一个点位于任何一个凸多面体外,但位于他们的组合模型内的情况。
Two-stage training
相较于虽然仅是一种估计,但是更易训练。在训练过程中,作者分为了两个步骤:
-
连续阶段:将所有的权重看作连续的值,通过计算一个大致的模型。
-
离散阶段:将权值离散化,通过在上的微调得到更加精确的结果。
Training Stage 1 - Continuous
初始化权值T与W,优化损失函数:
对于重建损失函数,给定一个查询点x,应与ground truth 相匹配,损失函数为:
对于矩阵T,用于将平面聚合为凸多面体,如果一个平面i与多面体j之间存在一条边,则,否则,,在这一训练阶段,T中元素被限制在[0,1]:
最后,对于矩阵W,希望其中的值尽可能接近1,但是在初始化时,矩阵W的值是近似为0的,这样做的目的是为了避免在训练过程中的梯度消失:
Training Stage 2 - Discrete
在离散阶段,首先先对矩阵T离散化,取一个较小的值,再执行,之后,再对网络进行微调:
在这一步训练过程中,论文中使用了来代替之前的以达到更好的效果,模型重建的损失函数为:
通过这一损失函数,使得当x位于模型内部时,趋向于0,否则,趋向于1。
为了防止产生的凸多面体相重叠,作者引入了一个新的函数,当时,代表x位于多个凸多面体内:
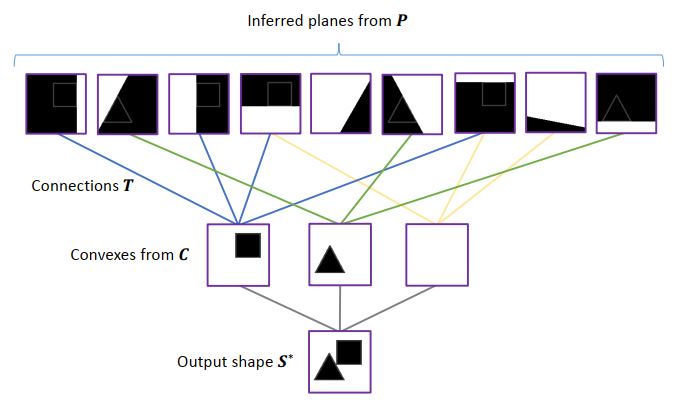
依然以二维几何模型为例,输入为一个二维的几何形状,经过两个阶段的优化后,输出结果如下图所示:
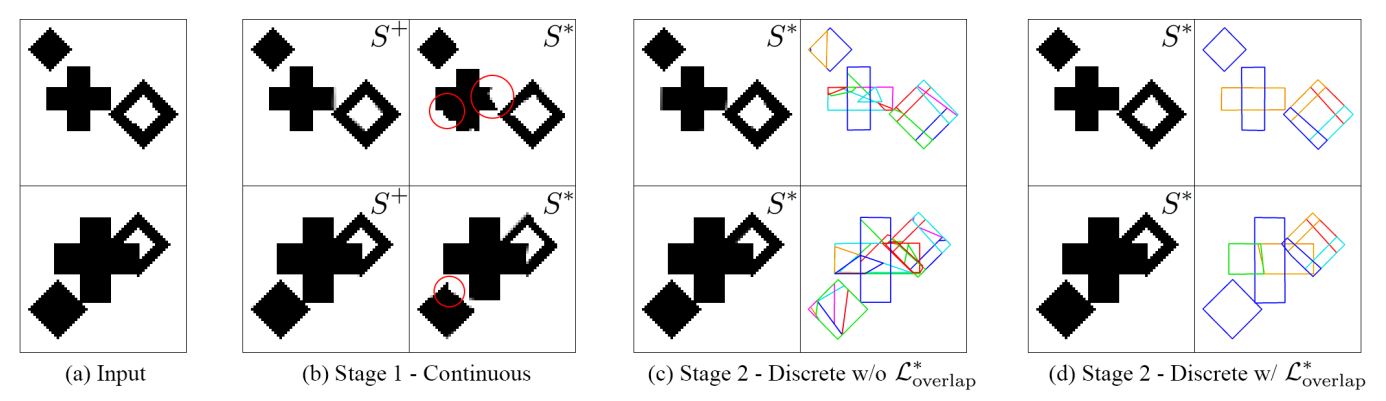
Conclusion
-
BSP-Net提出了一种利用BSP-Tree来表示三维模型的方法,对于输入的feature code,通过BSP-Net得到表示三维模型的BSP-Tree,再在树的基础上利用CSG建立多边形网格用于表示三维模型。在训练过程中,不需要多边形网格模型作为ground true参与训练,因此,网络的训练时self-supervised的,但依然需要依靠。
-
对于BSP-Tree这一种三维模型的表示方法,它是可被训练的,因为对于几何特征的编码采用了隐式函数的方法;而且,BSP-Tree的表示方法是可解释的,因为它的输出为凸多面体的集合。
-
这一表示方法可用于对三维模型的自编码、语义分割以及Single view reconstruction(SVR)等应用领域。
-
但是,BSP-Net对于凹面形状的处理是将其分割成多个凸多面体,这并不是一种特别好的处理方式。除此之外,BSP-Net的训练速度相对较慢。