参考论文

Mesh R-CNN

论文链接

Introduction

给定一张真实图片，论文提出了一种新的模型用于生成检测出的每一个物体的三角网格模型。这一模型被命名为Mesh R-CNN，是在Mask R-CNN的基础上添加了一个网格模型的预测分支用于生成具有各类拓扑结构的网格模型。论文提出，首先通过检测出的物体，粗略的生成这一物体的体素模型，之后再将体素模型转换为三角网格模型，最后通过图卷积网络生成更加真实的三维网格模型。之前的模型大多数专注于对类似ShapeNet而言，对单个物体进行渲染与生成，但是真实图片中的情况要更加复杂，图片内会有多个物体、物体间会有一些遮挡关系以及会有不同的光照条件的影响，这篇论文是对解决这一类问题的一种尝试。

对于三角网格模型的重建大部分方法采用通过一个template变形的方式生成目标三维模型，因此，生成的三维模型会与原始的模板具有相同的拓扑结构，这一方式在一定程度上限制了三维网格模型的生成质量。为解决这一问题，作者首先根据图像生成一个粗略的体素模型，再根据体素模型生成更加精细的三角网格模型。

Method

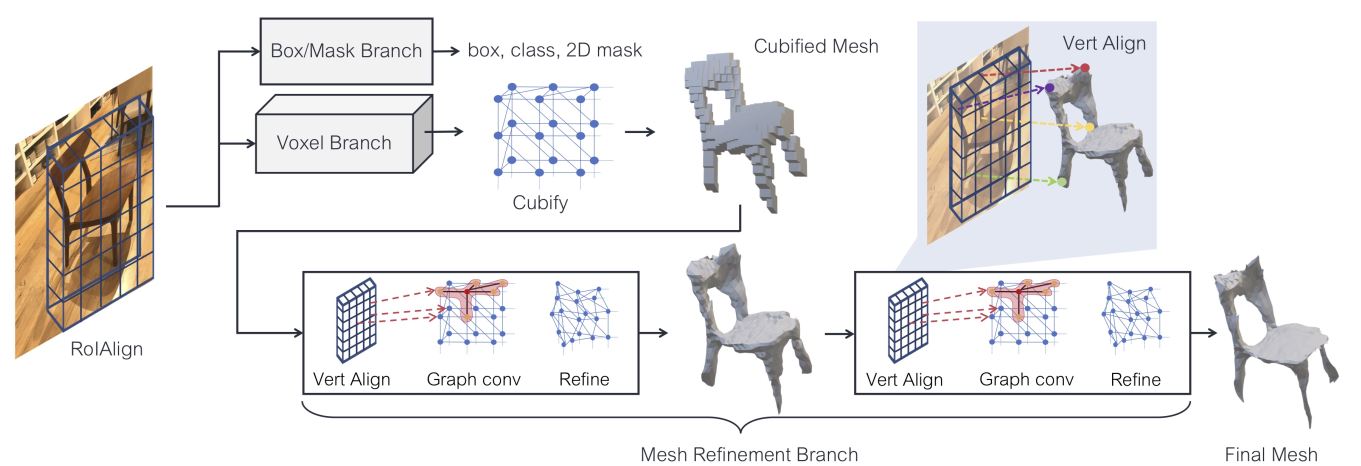
模型的整体结构如上图所示，为Mask R-CNN的拓展，在原始模型的基础上添加了voexl branch与mesh refinement branch，新添加的分支先由体素预测分支通过预选框对应的RolAlign预测物体的粗体素分布，并将粗体素转化为初始的三角网格，然后通过网格细化分支使用作用在网格顶点的图卷积层调整这个初始网格的顶点位置。

体素预测分支(Voxel Branch)

体素预测分支给出对每一个检测到的物体的粗体素模型，类似于Mask R-CNN在三维上的拓展，由对M×MM \times M网格内物体形状的预测转变为在G×G×GG \times G \times G的三维网格内对整个三维模型的预测。为了维持输入特征与预测体素之间的对应关系，论文在RoIAlign给出的输入特征图上添加了一个小的全卷积网络，这一卷积网络输出为具有G个通道的特征图，用于给出在输入的每一个位置每个体素是否被占据的概率。

Cubify：体素预测分支在给出粗体素模型之后，需要将其转换为三角网格模型，用于下一分支，这一过程被称为Cubify。每一个体素将其转换为具有8个顶点、18条边以及12个面的三角网格，之后，再将共享的顶点以及边通过合并与删除进而得到与体素模型有着同样拓扑结构的三角网格模型。

体素预测分支的loss函数为预测的体素模型与真实体素模型之间的交叉熵。

网格细化模型（Mesh Refinement Branch）

对于三角网格的细化操作分为了三个部分：顶点对齐（获得定点位置对应的图像特征）；图卷积（沿着网格边缘传播信息）；顶点细化（更新顶点位置）。

顶点对齐（Vertex Alignment）利用摄像机的intrinsic matrix将mesh中的每个顶点投影到二维图像上。给定特征图，对每一个投射的顶点计算它的双线性插值特征。

图卷积（Graph Convolution）将信息在网格点的边之间传递，卷积公式为：

fi′=ReLU(W0fi+∑j∈N(i)W1fj)f'_i = ReLU(W_0f_i + \sum_{j \in \mathcal{N}(i)}W_1f_j)

顶点细化（Vertex Refinement）用于更新三角网格的几何结构，更新公式如下所示：

vi′=vi+tanh(Wvert[fi;vi])v'_i = v_i + tanh(W_{vert}[f_i; v_i])

Mesh Loss：对于mesh重建的loss function的定义，论文从mesh的表面通过取样的方式得到点云，再通过点云来计算loss function。在采样过程中，根据每个三角形平面的面积抽取平面，然后使用两个随机变量σ1,σ2∼U(0,1)\sigma_1, \sigma_2 \sim U(0, 1)，采样点表示为：

p=w1v1+w2v2+w3v3p = w_1v_1 + w_2v_2 + w_3v_3

其中

w1=1−σ1,w2=(1−σ2)σ1,w3=σ2σ1w_1 = 1 - \sqrt{\sigma_1}, w_2 = (1 - \sigma_2)\sqrt{\sigma_1}, w_3 = \sigma_2\sqrt{\sigma_1}

给定两个点云P,QP,Q以及他们的法向量，令ΛP,Q={(p,argminq∣∣p−q∣∣):p∈P}\Lambda_{P,Q} = \{(p, argmin_q||p-q||) : p \in P\}表示点对(p,q)(p,q)的集合，其中q表示在点云Q中距离p最近的点，由此给出两个点云之间的chamfer distance为：

Lcham(P,Q)=∣P∣−1∑(p,q)∈ΛP,Q∣∣p−q∣∣2+∣Q∣−1∑(q,p)∈ΛQ,P∣∣q−p∣∣2\mathcal{L}_{cham}(P,Q) = |P|^{-1}\sum_{(p,q) \in \Lambda_{P,Q}}||p-q||^2 + |Q|^{-1}\sum_{(q, p)\in \Lambda_{Q,P}}||q-p||^2

两个点云之间的法向量距离为：

Lnorm(P,Q)=−∣P∣−1∑(p,q)∈ΛP,Q∣up⋅uq∣−∣Q∣−1∑(q,p)∈ΛQ,P∣uq⋅up∣\mathcal{L}_{norm}(P,Q) = -|P|^{-1}\sum_{(p,q) \in \Lambda_{P,Q}}|u_p \cdot u_q| - |Q|^{-1}\sum_{(q,p)\in \Lambda_{Q,P}}|u_q \cdot u_p|

添加一项形状正则化项防止网络退化：

Ledge(V,E)=1∣E∣∑(v,v′)∈E∣∣v−v′∣∣2\mathcal{L}_{edge}(V, E) = \frac{1}{|E|}\sum_{(v, v') \in E}||v - v'||^2

因此，mesh loss可写为：

Lmesh=Lcham(Pi,Pgt)+Lnorm(Pi,Pgt)+Ledge(Vi,Ei)\mathcal{L}_{mesh} = \mathcal{L}_{cham}(P^i, P^{gt}) + \mathcal{L}_{norm}(P^i, P^{gt}) + \mathcal{L}_{edge}(V^i, E^i)