CVPR2018 AtlasNet
参考论文
AtlasNet: A Papier-Mache Approach to Learning 3D Surface Generation
Introduction
曲面的形式定义为局部类似于欧几里得平面的拓扑空间,因此,作者在这篇论文中提出去通过一系列的平面映射到三维模型曲面的局部来估计整个目标曲面。这一工作介于利用少量的、固定的参数模块来表达一个三维物体以及利用大量无结构的点集来表示一个三维物体之间。也可以被理解为对曲面学习一种分解的表达方式,其中曲面上的点被编码模型结构的向量以及编码点的位置的向量所表示。通过将多个平面映射到三维物体上,理论上可以得到任意分辨率的三维模型,并且可以为生成的模型添加纹理映射。

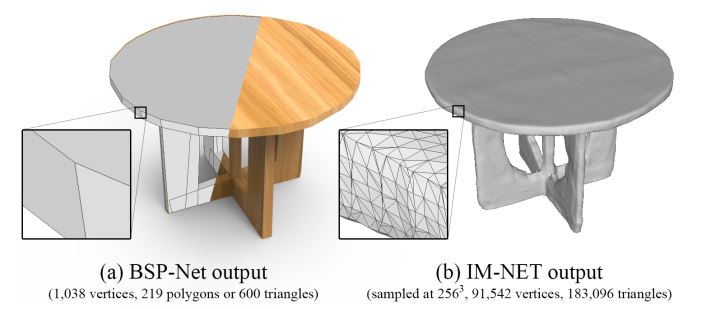
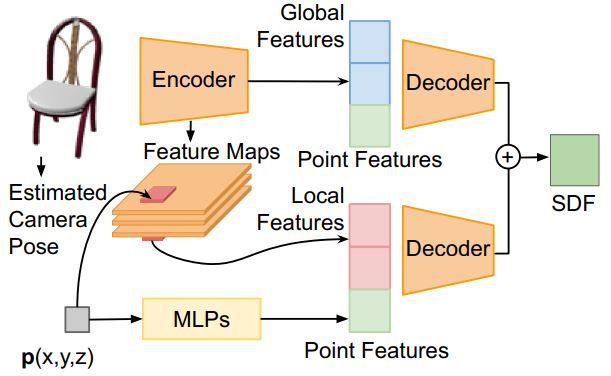
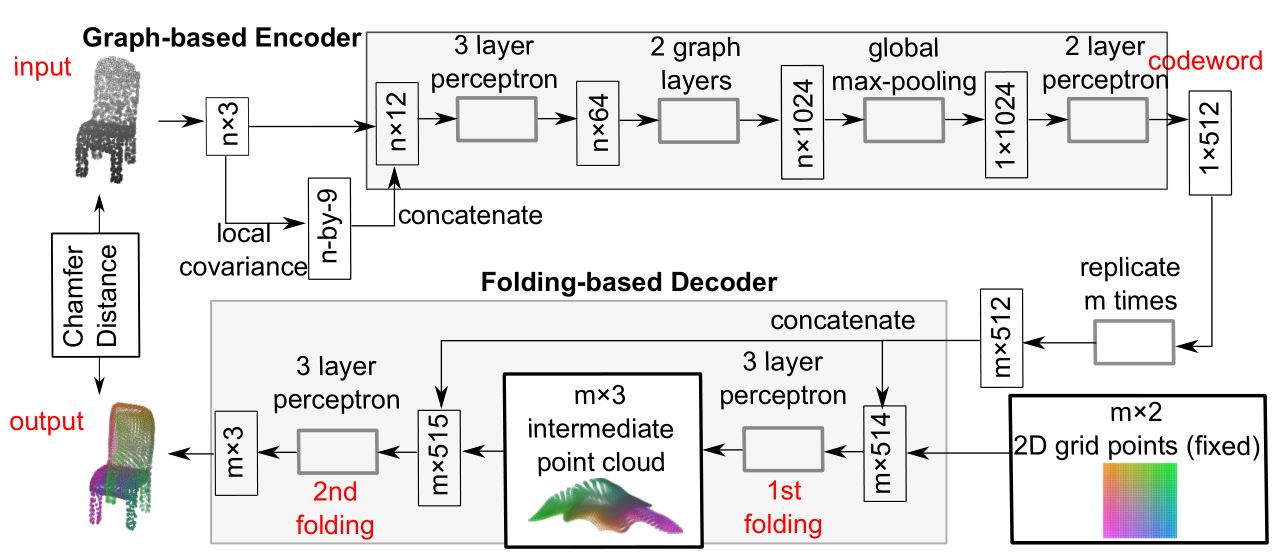
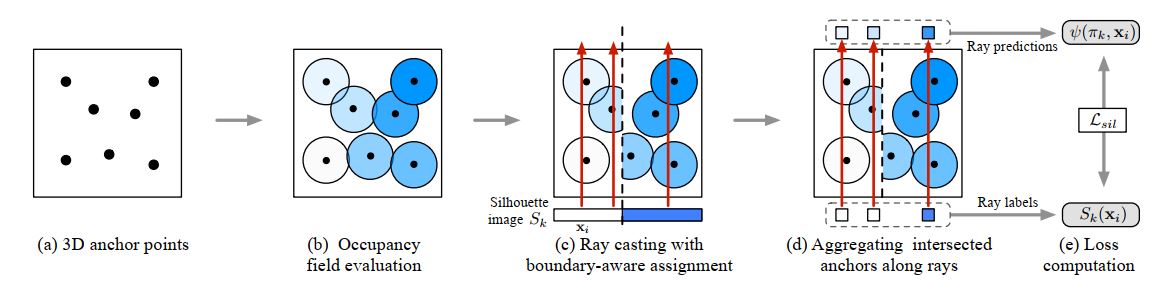
如上图所示,对于所有三维生成模型的方法而言,大致可被抽象为将隐含的模型表示作为输入,输出为生成的三维点的集合。图(a)即为最基本的方法,论文作者在此基础上在输入端添加了从一片平面上通过均匀取样的一个二维点,并利用这个二维点生成曲面上的一个点。因此,生成的模型就可以表示为一片连续的曲面。利用这一方法,网络也可以用来生成任意分辨率的三维模型。图(b)描述了上述方法。在图b的基础上进行扩展,将这一方法复制k次,则这一网络即可用于生成一系列的曲面用于构成最终的三维模型。
理论基础(Locally parameterized surface generation)
当对任意一个点,存在两个开集,使得与同胚, 则的一个子集是一个二维流形,即与低维欧氏空间拓扑同胚。从到的过程被称为chart,代表一个流形的微小局部,可被看作是欧几里得空间,其逆过程被称为参数化parameterization。能够覆盖整个二维流形的chart的二维图像集合被称为二维流形的地图集atlas。
学习生成一个局部的二维流形相当于找到一个参数化将一片二维的单位块映射到期望的二维流形上。用数学公式来表达,这一过程相当于最小化参数为\hteta的损失函数:
在具体实现时,则对二维流形采样,利用采样的点集计算Chamfer或者Earth-Mover距离。参数化函数通过多层感知机与ReLU激活层进行表示。
Proposition 1
令代表一个由多层感知机与ReLU组成的神经网络。则存在一个有限的多边形集合,使得对每一个,都是一个仿射函数:,其中。如果对于任意,有,则在多边形内的任一点p,存在一个邻域使得是一个二维流形。
这一用来估计二维流形局部的函数称为learnable parameterizations,这些函数的集合被称为learnable atlas。
Proposition 2
令S为可以被二维单位平面参数化的二维流形,对任意,存在一个整数K使得一个包含了ReLU激活函数以及K层隐含单元的多层感知机能够在误差之内估计S。
AtlasNet
Learning to decode a surface
给定一个三维模型的特征表示x,生成这一模型的曲面。给定N个learnable parametrizations ,为了训练参数,需要考虑如何计算生成模型与target之间的距离,以及怎样在MLP中运用模型的特征。
令为从二维单位平面上采样的点集,为从目标曲面上采样的点集。之后,将模型的特征向量x与采样的点的坐标连接起来作为MLP的输入。在训练过程中,最小化Chamfer loss:
Implementation details
对于对三维模型的自编码,给定输入为三维点云模型,利用PointNet作为编码器,将三维点云编码为隐含向量。对于通过图像生成三维模型的任务,利用ResNet-18作为编码器。对于解码器,采用四层全连接层,训练时,令输出点云大小始终为2500,以保证计算效率。