NeurIPS2019 Learning of Implicit Surfaces without 3D supervision

参考论文

Learning to Infer Implicit Surfaces without 3D Supervision

论文链接

Introduction

目前来说，我们拥有海量的二维图片，而三维模型的dataset相对来说较少，因此人们希望能够从二维图片中直接生成三维模型。对于主流的几种三维模型表示方法来说，点云与体素受限于模型的分辨率，三角网格难以有效地处理不同的拓扑结构。而Implicit Surfaces能够解决这些问题，但也存在难以构建三维与二维的联系、难以保证局部光滑的问题。这篇论文中，作者提出了ray-based field probing technique以及一个通用的geometric regularizer来解决上述问题，提出了一种仅通过二维图像来生成三维模型的框架。

对于显式的三维模型表示方法而言，能够很容易地将三维模型映射到二维图像上，反过来也很容易获得梯度流用于三维模型生成的监督学习。但是对于Implicit Surface而言，不能直接将其映射到二维平面上，而是采用ray sampling的方法，通过取样进行计算，但采用这种方法也会带来较大的计算成本。除此之外，Implicit Surface难以对三维模型的集合细节加以约束，与三角网格相比，Implicit Surface不能直接获得如法向量、曲率等几何信息。

这篇文章的主要贡献点在：

1. 提出了首个能够不使用3D信息进行监督学习Implicit Surfaces的框架

2. 提出了基于锚点以及探查射线的探查方法有效地将Implicit field与原始二维图像联系起来。

3. 提出了一种有效地取样方法用于implicit surface的生成。

4. 提出了一种通用的几何正则化项用于约束Implicit surface的几何特征。

Method

Overview

通过3D Ground Truth训练模型，能够提供关于曲面具体且连续的带符号的距离信息，但是二维图像仅能提供在三维空间是否被模型占据的部分信息。给定一个物体的$N_k$张来自不同视角$\{\pi_k\}_{k=1}^{N_K}$的图片$\{I_k\}_{k=1}^{N_K}$，训练一个网络，读取单张图片$I_k$，生成一个连续的表示空间被占据的概率的函数，其中概率为0.5的边界即表示该三维模型。这一方法基于ray-based field probing技术，大致框架如下图所示：

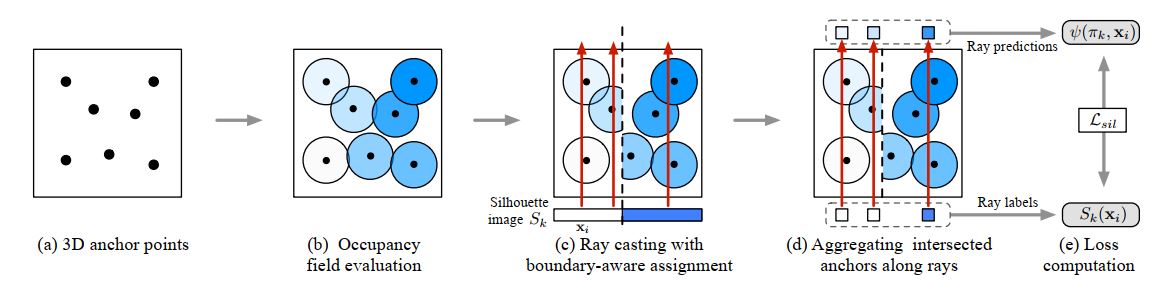
简单来说，首先在三维空间中进行取样避免不必要的计算，取样的点被称为锚点（anchor points）；之后，预测这些锚点被占用的概率，并将其作为球心假设球体内的点的占用概率均为这个值；之后通过探查射线（casting probing rays）建立三维空间中的点的占用情况与二维图像轮廓间的关系，具体来说，从viewpoint发出经过锚点的线，这些线与不同锚点的球相交，对射线上的占用概率做maxpooling得到被占用的情况映射到二维图像上。假设射线在viewpoint上经过二维图像上的点为$x_i$，给定相机参数$\pi_k$，得到预测值$\psi_{\pi_k, x_i}$与真实值$S_k(x_i)$，将其作为代价函数即可用于训练网络模型。

Network Architecture

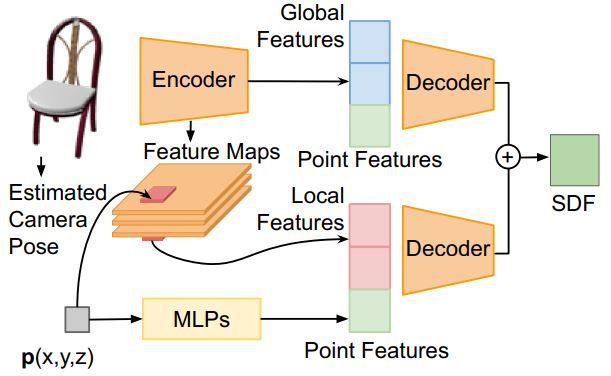
网络框架主要包含两个部分，第一部分为图像的编码器g将输入图像I编码为隐含特征z，第二部分为隐式曲面解码器f，输入为图像特征z以及一个特定的三维点$p_j$，输出为该点上被占用的概率$\phi(p_j)$，网络结构如下图所示：

Sampling-Based 2D Supervision

为了计算implicit decoder的预测误差，需要将每个ray穿过的occupancy field信息有效地聚合起来：给定一个occupancy field以及一个射线r上的锚点集合，则射线r能够穿过物体内部的概率可通过如下公式进行计算：

$$\psi(\pi_k, x_i) = \mathcal{G}(\{\phi(c + r(\pi_k, x_i) \cdot t_j)\}_{j=1}^{N_p})$$

其中，$r(\pi_k, x_i)$代表射线的方向，c表示相机的位置，$N_p$表示锚点的数量，$t_j$表示每一个锚点在射线上的位置，也可以理解为在三维空间中的采样点在射线上的映射，$\phi(\cdot)$表示occupancy function，对输入的三维点输出这一位置被占用的概率，$\psi$表示对射线$r(\pi_k, x_i)$被占用概率的预测，$\mathcal{G}$为最大池化函数。因此，得到关于三维模型框架的损失函数为$\mathcal{L}_{sil}$：

$$\mathcal{L}_{sil} = \frac{1}{N_r}\sum_{i=1}^{N_r}\sum_{k=1}^{N_K}||\psi(\pi_k, x_i) - S_k(x_i)||^2$$

Boundary-Aware Assignment

在之前的介绍中，为了减少射线与点相交的计算量，作者将三维空间中采样的锚点看作半径不为零的球体，使得射线与球体相交。但是这样做存在一定的问题，不穿过物体的射线仍有可能穿过位于三维物体内部的锚点所代表的球体，造成对射线的标记错误。论文通过利用二维轮廓的信息，将这些会干扰标记结果的锚点过滤掉，例如射线穿过位于二维轮廓内/外的像素点且锚点位于三维物体外/内，则这样的锚点就会在计算射线与锚点交叉的过程中被忽略掉。

Importance Sampling

三维物体对整个三维空间来说是稀疏的，通过随机采样选择锚点的方法会非常低效，因此论文中依据重要性对锚点进行采样，即三维物体表面区域应采样更多的锚点以及射线。在取样过程中，首先获得二维模型轮廓的映射，即对输入的轮廓乘上拉普拉斯算子，得到$W_r(x)$，对每个的像素施加一个高斯分布核，构成一个混合高斯模型，之后的取样就通过这一混合高斯模型进行，锚点取样以及射线取样的概率密度函数为：

$$\left\{ \begin{array}{ll} P_r(x) = \int_{x'}\kappa(x',x;\sigma)W_r(x')dx' \\ P_p(p) = \int_{p'}\kappa(p',p;\sigma)W_r(p')dp' \end{array} \right.$$

其中，$x'$表示在二维图像上的像素，$p'$表示在三维空间中的点。

Geometric Regularizaiton on Implicit Surface

对隐式空间内的点$p_j$求n阶导：

$$\frac{\delta^n \phi}{\delta p^n_j} = \frac{1}{\Delta d^n}\sum_{l=0}^{n}(-1)^l\binom{n}{l}\phi(p_j + (\frac{n}{2} - l)\Delta d)$$

其中，$\Delta d$表示点$p_j$到它临近的采样点的空间距离，n=1，则曲面的法向量$n(p_j)$可通过公式$n(p_j) = \frac{\delta \phi}{\delta p_j} / |\frac{\delta \phi}{\delta p_j}|$计算得到。

但是，并不是所有的点都应具有相同的权重，在三维模型重建的过程中，我们更关注于位于三维模型表面上的点，因此，对这些点添加一个权重$W(x) = \mathbb{I}(|x - 0.5|) < \epsilon$，得到loss function为：

$$\mathcal{L}_{geo} = \frac{1}{N_p}\sum_{j=1}^{N_p}W(\phi(s_j))\frac{\sum_{l=1}^6W(\phi(q_j^l))||n(s_j) - n(q_j^l)||^p_p}{\sum_{l=1}^6W(\phi(q_j^l))}$$

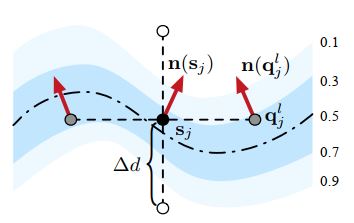
如上图所示，对每一个锚点$s_j$，选择在一定范围内的两个临近点，对每个锚点乘权重函数，使得越接近模型表面的锚点有越高的权重。通过最小化正则化项，使得临近的锚点趋向于拥有相近的法向量。

因此，整个网络训练的损失函数包含了轮廓损失函数以及集合正则化损失函数为：

$$\mathcal{L} = \mathcal{L}_{sil} + \lambda\mathcal{L}_{geo}$$