参考论文

DISN: Deep Implicit Surface Network for High-quality Single-view 3D Reconstruction

论文链接

Introduction

本文提出了一种新的从二维图片中重建三维模型的方法，通过预测三维空间中的符号距离来从二维图片中生成具有更高细节质量的三维网格模型。与其他方法只能够重建物体的整体结构相比， DISN重建出的模型具有更好的细节，例如模型中的孔以及模型中比较细的结构，重建效果如下图所示：

在这篇论文中，为解决其他三维表示方法分辨率不高，拓扑结构不能改变，难以描述物体的具体细节等问题，作者选择学习一种隐含的三维曲面的表示方法，被称为Signed Distance Functions(SDF)。SDF把从三维空间中取样得到的点编码为到物体表面上带符号的距离。因此，只需要给定一个带符号距离值的集合，就能够从其中提取到对应的三维模型。

为解决生成模型细节的问题，作者引入了局部特征提取模块，首先，模型将从输入的图像中提取视角的参数，之后利用这些信息将每个查询的点投影到输入的图像上来识别相应的local patch，再从local patch提取局部特征并与全局特征结合预测这些三维点的SDF值。

Method

对于SDF的解释如下图所示:

SDF

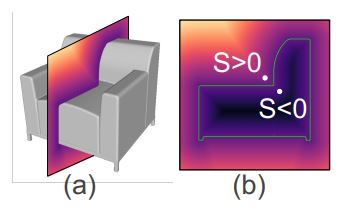
SDF相当于一个连续的函数，将给定的空间中的点p=(x,y,z)∈R3p = (x, y, z) \in \mathbb{R}^3映射到一个实数s∈R:s=SDF(p)s \in \mathbb{R}: s = SDF(p)。s的绝对值表示点到曲面的距离，s的符号表示点在曲面外还是曲面内。则曲面S0={p∣SDF(p)=0}\mathcal{S}_0 = \{p | SDF(p) = 0\}即可用于代表一个三维的物体。

DISN: Deep Implicit Surface Network

DISN的整体结构如下图所示：


DISN

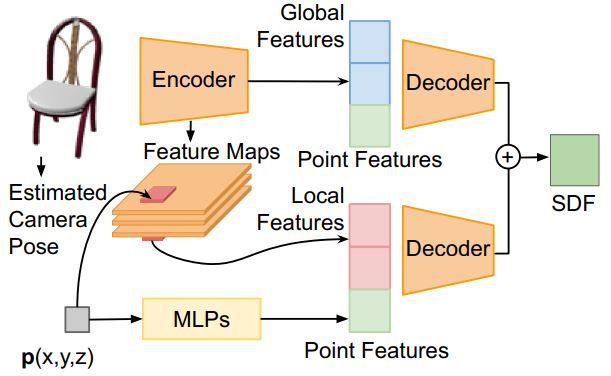
DISN网络被分为两个部分：相机姿态估计以及SDF预测。首先，通过二维图像预测三维模型投影到二维图像所对应的相机参数，再通过预测的参数将每一个三维点投影到二维平面上并在每层上提取对应的局部特征。最后，DISN将根据多层的局部特征以及全局特征将给定的空间中的点解码为对应的SDF值。

Camera Pose Estimation

给定一张二维图像作为输入，目标是估计对应的视点信息，作者采用一个六维向量表示物体的旋转信息，向量为b=(bx,by)\bm{b} = (\bm{b_x}, \bm{b_y})，其中b∈R6,bx∈R3,by∈R3\bm{b} \in \mathbb{R}^6, \bm{b_x} \in \mathbb{R}^3, \bm{b_y} \in \mathbb{R}^3。给定向量b\bm{b}，则旋转矩阵可以被表示为：

R=(Rx,Ry,Rz)T∈R3×3\bm{R} = (\bm{R_x}, \bm{R_y}, \bm{R_z})^T \in \mathbb{R}^{3 \times 3}

Rx=N(bx),Rz=N(Rx×by),Ry=Rz×Rx\bm{R_x} = N(\bm{b_x}), \bm{R_z} = N(\bm{R_x} \times \bm{b_y}), \bm{R_y} = \bm{R_z} \times \bm{R_x}

其中Rx,Ry,Rz∈R3\bm{R_x}, \bm{R_y}, \bm{R_z} \in \mathbb{R}^3，N(⋅)N(\cdot)是标准化函数。平移向量t∈R3\bm{t} \in \mathbb{R}^3则通过网络直接得出。相机参数预测网络的结构如下图所示：


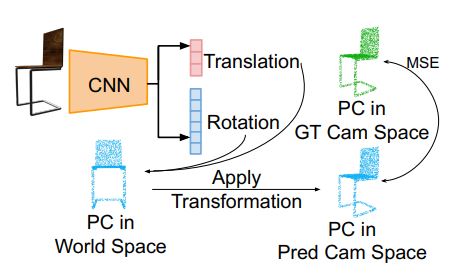
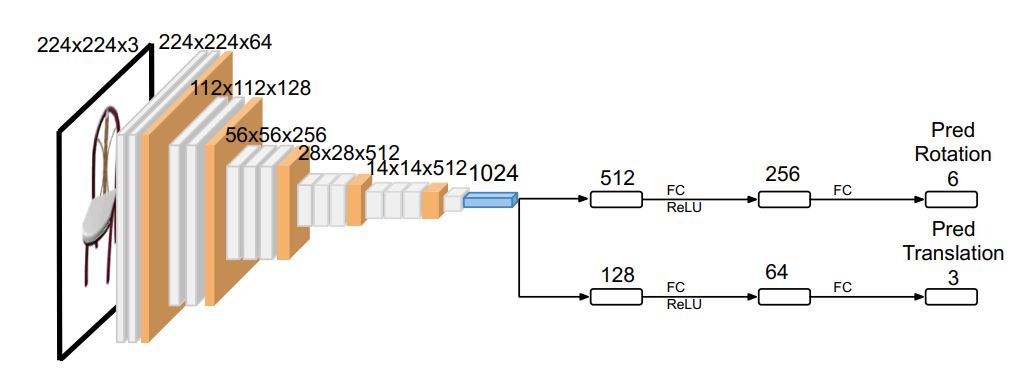
对于代价函数的计算，作者将预测出的相机参数作用在原始的点云上，再与ground truth进行比较，代价函数的公式为：

Lcam=∑pw∈PCw∣∣pG−(Rpw+t)∣∣22∑pw∈PCw1L_{cam} = \frac{\sum_{\bm{p}_w \in PC_w}||\bm{p}_G - (\bm{Rp}_w + \bm{t})||^2_2}{\sum_{\bm{p}_w \in PC_w}1}

SDF Prediction with Deep Neural Network

Local Feature Extraction

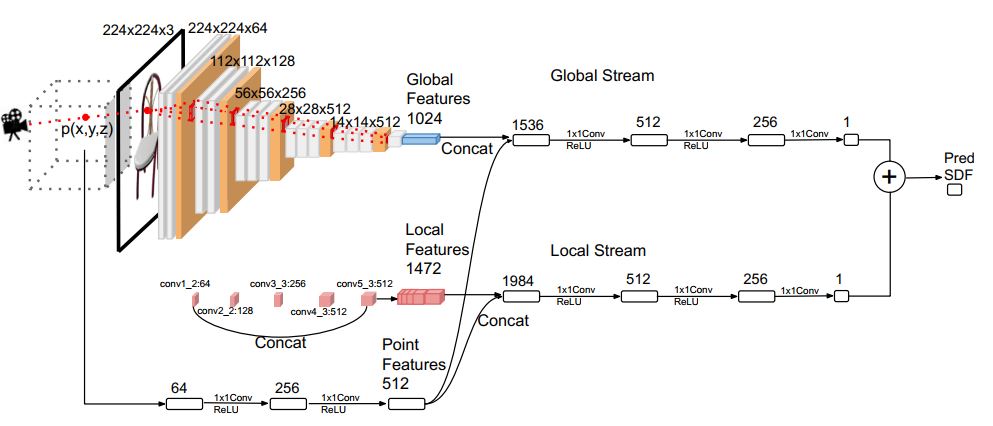
为了能够在重建的三维模型上展示更加具体的细节，因此需要在网络中添加对局部特征的提取。对局部特征的提取，如下图所示：

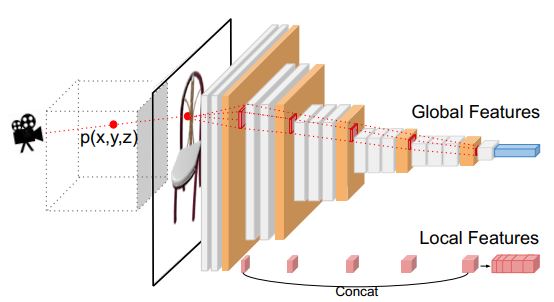
三维的点p∈R3\bm{p} \in \mathbb{R}^3被投影到二维平面上的点q∈R2\bm{q} \in \mathbb{R}^2上，之后，将网络中每一层上q\bm{q}位置上的局部特征取出并连接在一起构成局部特征。

之后，两个解码器分别以全局特征以及局部特征作为输入预测出给定点的SDF值。

Loss Function

LSDF=∑pm∣f(I,p)−SDFI(p)∣,L_{SDF} = \sum_{p}m|f(I, \bm{p}) - SDF^I(p)|,

m={m1,if SDFI(p)<δm2,otherwisem = \left\{ \begin{array}{ll} m_1, & if \ SDF^I(\bm{p}) < \delta \\ m_2, & otherwise \end{array} \right.

Surface Reconstruction