参考论文
C3DPO: Canonical 3D Pose Networks for Non-Rigid Sturcture From Motion
论文链接
Introduction
C3DPO用于从2D的关键点的标注中提取并建立对于可变形物体的三维模型。与其他同类方法不同的是,C3DPO的训练不需要三维的信息。
C3DPO通过神经网络从二维图像中的关键点分解得到模型的视角、变形等信息,的主要贡献在于:(1)在重建三维标准模型以及视角的过程中仅使用了单一图片中的二维关键点。(2)使用一种新的自监督的限制将三维的形状以及二维的视角分离。(3)可以处理在观察过程中被遮挡的部分。(4)在多种不同类的物体上都有很好的表现。
Overview
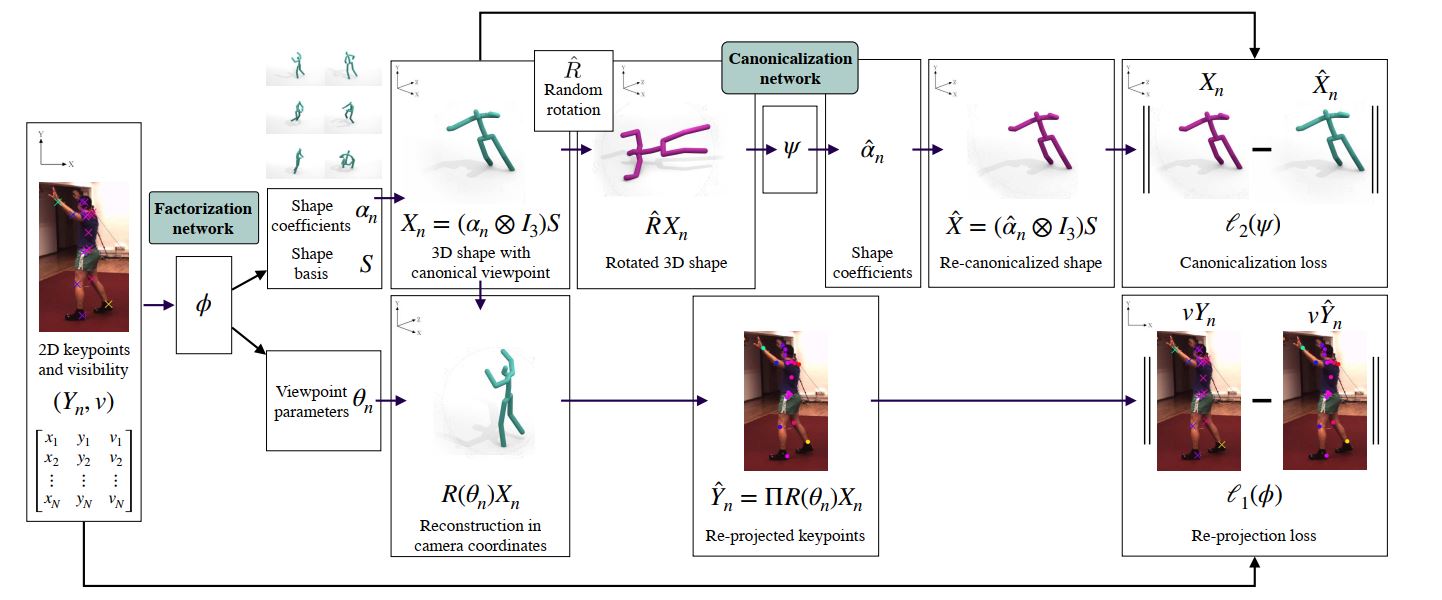
C3DPO的整体结构如下图所示:
Method
Sturcture from motion(SFM)
SFM的输入为元组y n = ( y n 1 , … , y n K ) ∈ R 2 × K y_n = (y_{n1}, \dots, y_{nK}) \in \mathbb{R}^{2 \times K} y n = ( y n 1 , … , y n K ) ∈ R 2 × K y n y_n y n X = ( X 1 , … , X K ) ∈ R 3 × K X = (X_1, \dots, X_K) \in \mathbb{R}^{3 \times K} X = ( X 1 , … , X K ) ∈ R 3 × K ( R n , T n ) ∈ S O ( 3 ) × T ( 3 ) (R_n, T_n) \in SO(3) \times T(3) ( R n , T n ) ∈ SO ( 3 ) × T ( 3 ) y n k = Π ( R n X k + T n ) y_{nk} = \Pi(R_nX_k + Tn) y nk = Π ( R n X k + T n ) Π : R 3 − R 2 \Pi : \mathbb{R}^3 - \mathbb{R}^2 Π : R 3 − R 2 Π = [ I 2 , 0 ] \Pi = [I_2, 0] Π = [ I 2 , 0 ] y n k = M n X k = Π R n X k y_{nk} = M_nX_k = \Pi R_n X_k y nk = M n X k = Π R n X k
Y = [ y 11 ⋯ y 1 K ⋮ ⋱ ⋮ y N 1 ⋯ y N K ] , M = [ M 1 ⋮ M N ] , Y = M X . Y =
\begin{bmatrix}
y_{11} & \cdots & y_{1K} \\
\vdots & \ddots & \vdots \\
y_{N1} & \cdots & y_{NK}
\end{bmatrix},
M =
\begin{bmatrix}
M_1 \\
\vdots \\
M_N
\end{bmatrix},
Y = MX.
Y = y 11 ⋮ y N 1 ⋯ ⋱ ⋯ y 1 K ⋮ y N K , M = M 1 ⋮ M N , Y = MX .
因此,从上述式子中可以看出,SFM可以被公式表达为将物体的视图Y分解为观察点M(viewpoint)以及结构X(structure)。但是,对于矩阵Y的分解,并不是唯一的,需要添加一些限制条件以保证矩阵分解的歧义最小。由等式M X = ( M A − 1 ) ( A X ) MX = (MA^{-1})(AX) MX = ( M A − 1 ) ( A X ) ( M A − 1 , A X ) (MA^{-1}, AX) ( M A − 1 , A X ) 2 N K ≥ 6 N + 3 K − 9 2NK \ge 6N + 3K - 9 2 N K ≥ 6 N + 3 K − 9
Non-rigid sturcture from motion
NR-SFM与SFM相似,但是NR-SFM能够允许物体的结构X n X_n X n X n = X ( α n ; S ) X_n = X(\alpha_n ; S) X n = X ( α n ; S ) α n ∈ R D \alpha_n \in \mathbb{R}^D α n ∈ R D S ∈ R 3 D × K S \in \mathbb{R}^{3D \times K} S ∈ R 3 D × K
X ( α n ; S ) = ( α n ⊗ I 3 ) S X(\alpha_n; S) = (\alpha_n \otimes I_3)S
X ( α n ; S ) = ( α n ⊗ I 3 ) S
其中α \alpha α ⊗ \otimes ⊗ X = ( α ⊗ I 3 ) S ∈ R 3 N × K , α ∈ R N × D X = (\alpha \otimes I_3)S \in \mathbb{R}^{3N \times K}, \alpha \in \mathbb{R}^{N \times D} X = ( α ⊗ I 3 ) S ∈ R 3 N × K , α ∈ R N × D
给定关键点的多个视角,NR-SFM的目标就是从这些视角中恢复出物体的动作以及基本的形状。这一等式可被表示为:
y n k = Π ( R n ∑ d = 1 D α n d S d k + T n ) y_{nk} = \Pi(R_n\sum_{d=1}^D\alpha_{nd}S_{dk} + T_n)
y nk = Π ( R n d = 1 ∑ D α n d S d k + T n )
同样的,对其进行中心化,得到公式如下所示:
Y = M ˉ ( α ⊗ I 3 ) S , ( Y ∈ R 2 N × K , M ˉ ∈ R 2 N × 3 N ) Y = \bar{M}(\alpha \otimes I_3)S, (Y \in \mathbb{R}^{2N \times K}, \bar{M} \in \mathbb{R}^{2N \times 3N})
Y = M ˉ ( α ⊗ I 3 ) S , ( Y ∈ R 2 N × K , M ˉ ∈ R 2 N × 3 N )
矩阵M ˉ \bar{M} M ˉ M ˉ = d i a g ( M 1 , … , M N ) \bar{M} = diag(M_1, \dots, M_N) M ˉ = d ia g ( M 1 , … , M N )
Monocular motion and structure estimation
根据上述等式,一旦shape basis S被学习到,就可以通过物体单一的视图Y去重建viewpoint以及pose。但是,这一想法仍需要解决矩阵分解的问题。
在C3DPO中,希望训练一个映射关系:
Φ : R 2 K × { 0 , 1 } K → D × R 3 , ( Y , v ) → ( α , θ ) \Phi : \mathbb{R}^{2K} \times \{0, 1\}^{K} \to \mathbb{D} \times \mathbb{R}^3, (Y, v) \to (\alpha, \theta)
Φ : R 2 K × { 0 , 1 } K → D × R 3 , ( Y , v ) → ( α , θ )
其中,v是由布尔值组成的行向量,表示在给定的视图中,对应的关键点是否能够被看到。这一映射的输出为D维的姿态参数α \alpha α θ ∈ R 3 \theta \in \mathbb{R}^3 θ ∈ R 3 θ \theta θ M ( θ ) = Π R ( θ ) = Π e x p m [ θ ] × M(\theta) = \Pi R(\theta) = \Pi expm[\theta]_{\times} M ( θ ) = Π R ( θ ) = Π e x p m [ θ ] ×
与其他方法相比,通过对这一映射的学习,可以包含在线性模型中不明显的物体结构信息。对于这一映射的学习,通过最小化re-projection loss来实现:
l 1 ( Y , v ; Φ , S ) = 1 K ∑ k = 1 K v k ⋅ ∣ ∣ Y k − M ( θ ) ( α ⊗ I 3 ) S : , k ∣ ∣ ϵ \mathcal{l}_1(Y, v; \Phi, S) = \frac{1}{K} \sum_{k=1}^{K}v_k \cdot ||Y_k - M(\theta)(\alpha \otimes I_3)S_{:, k}||_{\epsilon}
l 1 ( Y , v ; Φ , S ) = K 1 k = 1 ∑ K v k ⋅ ∣∣ Y k − M ( θ ) ( α ⊗ I 3 ) S : , k ∣ ∣ ϵ
其中,( α , θ ) = Φ ( Y , v ) , ∣ ∣ z ∣ ∣ ϵ = ( 1 + ( ∣ ∣ z ∣ ∣ / ϵ ) 2 − 1 ) ϵ (\alpha, \theta) = \Phi(Y, v),||z||_{\epsilon} = (\sqrt{1+ (||z||/\epsilon)^2}-1){\epsilon} ( α , θ ) = Φ ( Y , v ) , ∣∣ z ∣ ∣ ϵ = ( 1 + ( ∣∣ z ∣∣/ ϵ ) 2 − 1 ) ϵ
Consistent factorization via canonicalization
对于NR-SFM来说,最大的挑战在于分解三维模型的视点的变化以及模型的变形带来的歧义。在这一部分中,作者提出了一种新的方法,直接去鼓励网络生成一致的模型。通常,令X 0 \mathcal{X}_0 X 0 X ( α ; S ) X(\alpha; S) X ( α ; S ) X , X ′ ∈ X 0 X, X' \in \mathcal{X}_0 X , X ′ ∈ X 0 X ′ = R X X' = RX X ′ = RX Ψ : R 3 × K → R 3 × K \Psi :\mathbb{R}^{3 \times K} \to \mathbb{R}^{3 \times K} Ψ : R 3 × K → R 3 × K ∀ R ∈ S O ( 3 ) , X ∈ X 0 , X = Ψ ( R X ) \forall R \in SO(3), X \in \mathcal{X}_0, X = \Psi(RX) ∀ R ∈ SO ( 3 ) , X ∈ X 0 , X = Ψ ( RX )
在C3DPO中,为保证能够将视点与物体的姿态有效地区分开,引入loss function为:
l 2 ( X , R ; Ψ ) = 1 K ∑ k = 1 K ∣ ∣ X : , k − Ψ ( R X ) : , k ∣ ∣ ϵ \mathcal{l}_2(X, R; \Psi) = \frac{1}{K}\sum_{k=1}^{K}||X_{:,k} - \Psi(RX)_{:,k}||_{\epsilon}
l 2 ( X , R ; Ψ ) = K 1 k = 1 ∑ K ∣∣ X : , k − Ψ ( RX ) : , k ∣ ∣ ϵ
其中,R ∈ S O ( 3 ) R \in SO(3) R ∈ SO ( 3 )
在网络训练过程中,输入为Y n Y_n Y n Φ ( Y n , v ) \Phi(Y_n, v) Φ ( Y n , v ) θ n \theta_n θ n α n \alpha_n α n R ^ \hat{R} R ^ X n = X ( α n ; S ) X_n = X(\alpha_n; S) X n = X ( α n ; S ) R ^ X n \hat{R}X_n R ^ X n Ψ \Psi Ψ α ^ n \hat{\alpha}_n α ^ n R ^ \hat{R} R ^ X ^ n = X ( α ^ n ; S ) \hat{X}_n = X(\hat{\alpha}_n; S) X ^ n = X ( α ^ n ; S ) X n X_n X n l 2 l_2 l 2 Φ \Phi Φ Ψ \Psi Ψ l 1 + l 2 l_1+l_2 l 1 + l 2
In-plane rotation invariance
根据旋转不变性,能够进一步为神经网络添加约束用于学习。令Y = Π R X Y = \Pi RX Y = Π RX r z ∈ S O ( 2 ) r_z \in SO(2) r z ∈ SO ( 2 ) Φ ( Y , v ) = ( α , θ ) \Phi(Y, v) = (\alpha, \theta) Φ ( Y , v ) = ( α , θ ) Φ ( r z Y , v ) = ( α ′ , θ ′ ) \Phi(r_zY, v) = (\alpha' , \theta') Φ ( r z Y , v ) = ( α ′ , θ ′ ) α = a l p h a ′ \alpha = alpha' α = a lp h a ′
l 3 ( Y , v ; Φ , S ) = 1 K ∑ k = 1 K v k ∣ ∣ r z Y k − M ( θ ′ ) ( α ⊗ I 3 ) S : , k ∣ ∣ ϵ l_3(Y, v; \Phi, S) = \frac{1}{K}\sum_{k=1}^{K}v_{k} ||r_zY_k - M(\theta')(\alpha \otimes I_3)S_{:,k}||_{\epsilon}
l 3 ( Y , v ; Φ , S ) = K 1 k = 1 ∑ K v k ∣∣ r z Y k − M ( θ ′ ) ( α ⊗ I 3 ) S : , k ∣ ∣ ϵ
因此,最终的loss修改为l 2 + l 3 l_2+l_3 l 2 + l 3
(论文里提到Φ ( Y , v ) = ( α , θ ) \Phi(Y, v) = (\alpha, \theta) Φ ( Y , v ) = ( α , θ ) Φ ( r z Y , v ) = ( α ′ , θ ′ ) \Phi(r_zY, v) = (\alpha' , \theta') Φ ( r z Y , v ) = ( α ′ , θ ′ )