ICCV2019 PU-GAN

参考论文

PU-GAN: a Point Cloud Upsampling Adversarial Network

论文链接

Introductin

通过扫描仪等设备所获得的三维模型的点云通常是稀疏的、有噪音的、不均匀的，因此，在对这一类的点云数据进行进一步处理之前， 需要通过一些方式对其进行修改，生成密集、完整、均匀的点云集合。在这片论文中，作者提出了一种新型的点云upsampling框架，并命名为PU-GAN。

Method

Overview

给定一个无序的点击$\mathcal{P} = \{p_i\}^N_{i=1}$，期望生成一个更加密集的点集$\mathcal{Q} = \{q_i\}^{rN}_{i=1}$，其中r被称为上采样率。对于生成的点击Q，需要满足两个条件：

1. 输出Q与输入P应该对一个目标物体描述了同样的集合特征，因此在集合Q中的点应该分布并且覆盖在目标物体的表面。

2. 即使输入P中的点是稀疏并且不均匀的，输出Q上的点也应该均匀分布在目标物体的表面

PU-GAN的网络结构如下所示：

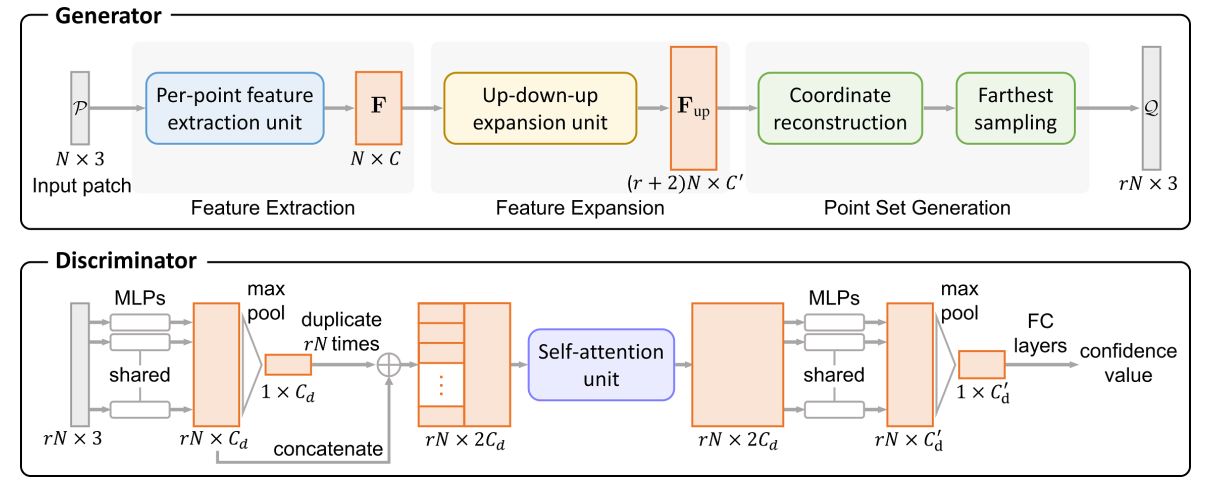
网络结构 Network Architecture

生成器 Generator

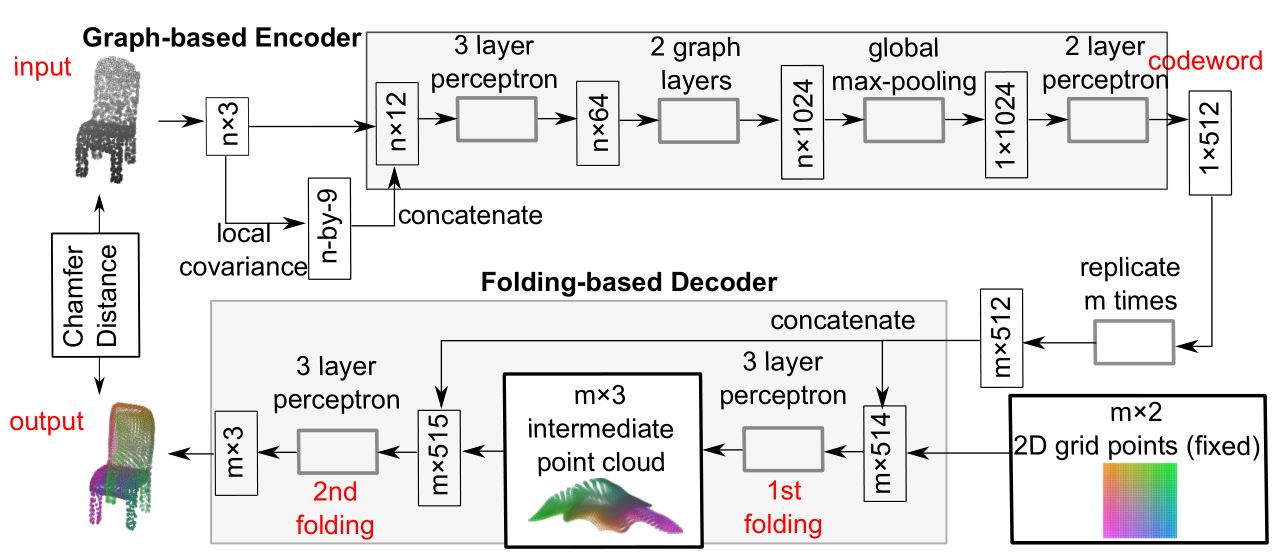
在生成器中，论文中主要通过三个部分对输入点集P进行处理：特征提取模块、特征扩展模块以及点集生成模块。

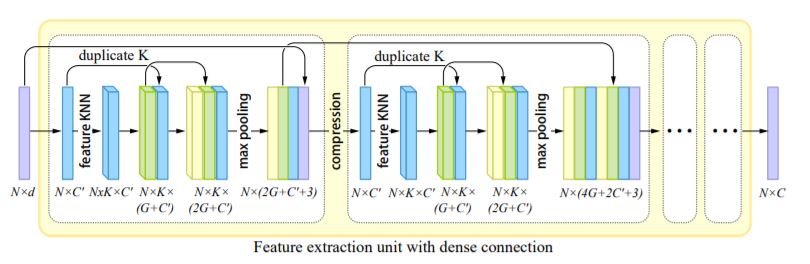
特征提取模块(The feature extraction component)用于从输入集合$\mathcal{P} \in \mathbb{R}^{N \times d}$中提取特征信息F，其中d表示输入点属性（坐标、颜色、法向量等）的维度，在这里，n=3。对于特征提取网络，作者采用Patch-based progressive 3D point set upsampling中所提出的方法，特征提取模块的网络结构如下图所示，这一网络采用dese connection，网络中的操作被分为一系列的dese block，中间值通过dese connection在block内与block间相连接，这样保证了在每一层提取的特征能够被重复利用，以此可以在小的模型规模上同样产生好的重建效果。

特征扩展模块(The feautre expansion component)将提取的特征F扩展为$F_{up}$，在这一模块中，论文提出了up-down-up expansion unit来提高$F_{up}$的方差，使得生成器能够生成更多不同种类的点集分布。

点集生成模块（The point set generation component）首先通过MLP将特征$F_{up}$回归到三维坐标的集合上，之后通过farthest sampling取样出$rN$个点作为最终生成器生成的点集，这也是之前$F_{up}$具有$(r+2)N$个特征的原因。

判别器 Discriminator

判别器的目标是判断输入的点集是否是生成器所生成的。判别器中首先采用了论文（PCN: Point completion network）中提出的网络来进行特征提取，这一网络结构能够有效地提取全局以及局部的特征信息，并确保了一个轻量的网络结构，其结构如下所示：

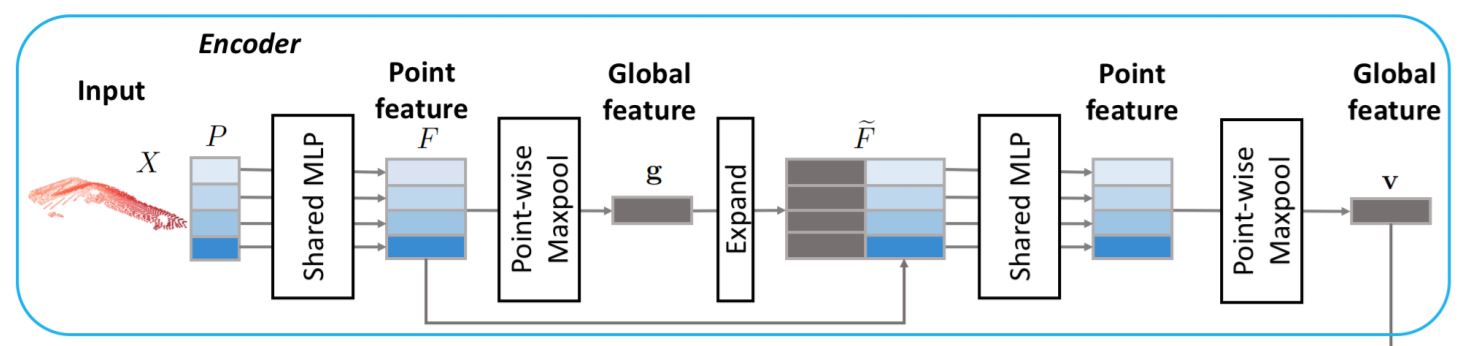
判别器中特征提取网络的输入为点集P，其中的每一行表示点集中一个点的坐标信息，之后的共享MLP包含了两层线性连接层并通过ReLU激活函数连接，用于将每个点$p_i$转换为点的特征$f_i$，之后得到了点集的特征矩阵$F$，再经过最大池化层得到k维的全局特征$g$。之后再将全局特征与每个点的局部特征相连接，组成新的特征矩阵$\widetilde{F}$。

论文（PCN: Point completion network）提出的网络共有两层PN层，在PU-GAN中，作者在两层之间加入了self-attention unit以提升对特征的学习能力，并在最后加入全连接层得到confidence值。

Up-down-up Expansion Unit

Up-down-up Expansion Unit结构图如下所示：

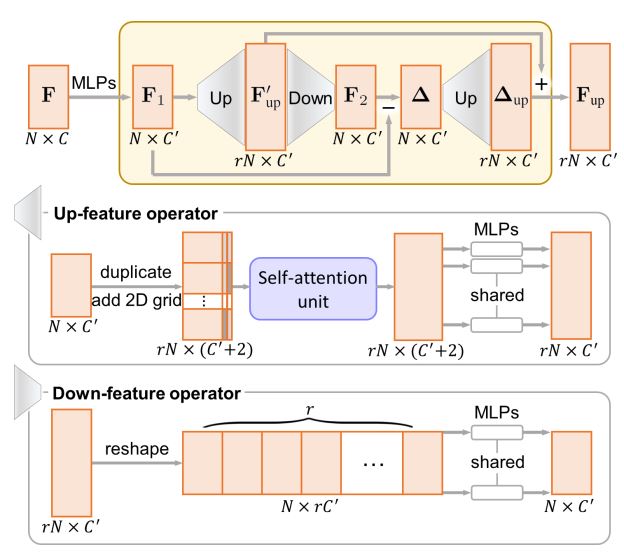
在这一部分中，网络首先将点集特征$F_{up}$经过上采样生成$F'_{up}$，再经过下采样回到原来点集特征的大小，记作$F_2$，之后将经过上下采样后的特征与原始的特征进行比较，计算出差值$\Delta$，之后将$\Delta$经过上取样生成$\Delta_{up}$与$F'_{up}$相加，得到最终的上取样结果$F_{up}$。

Up-feature operator

为了能够对点的feature进行上采样，需要将复制了r次的特征间的方差尽可能大，也就是说，需要使得新采样的点与原始点之间的距离尽可能大一些。在复制了特征矩阵r次之后，利用FoldingNet的思想，对每一个复制的特征连接一个独有的二维向量。之后再经过self-attention unit与MLP之后输出上取样后的特征矩阵。

Down-feature operator

为了进行下取样，将上取样后的特征矩阵$F_{up} \in \mathbb{R}^{rN \times C'}$变形为$\mathbb{R}^{N \times rC'}$。再经过MLP之后得到原始的特征。

Self-attention Unit

为了在特征中引入大范围的context的关联关系去提高特征的整体性，论文里在生成器和判别器中都加入了self-attention unit，自注意力模块的结构如下所示：

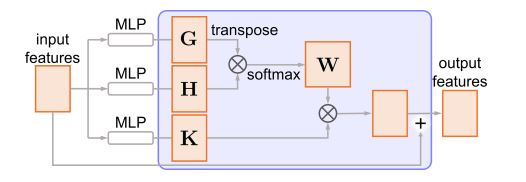
首先将特征矩阵经过三个不同的MLP转换成G、H与K，之后再通过G与H计算出注意力权重W:

$$W = f_{softmax}(G_TH)$$

之后，就可以得到权重特征$W^TK$，最终，计算出的权重特征矩阵与原始的特征矩阵相加，即得到最终的输出。

Loss function

Adversarial loss

$$\mathcal{L}_{gan}(G) = \frac{1}{2}[D(\mathcal{Q}) - 1]^2$$

$$\mathcal{L}_{gan}(D) = \frac{1}{2}[D(\mathcal{Q})^2 + (D(\hat{\mathcal{Q}}) - 1)^2]$$

其中$D(\mathcal(Q))$表示由生成器生成的点集$\mathcal{Q}$通过判别器D之后的confidence值。

Uniform loss

为使得最后生成的点云集合在目标物体的表面上分布均匀，需要设计Uniform loss来满足这一要求。论文中提到，在网络的训练中，首先通过farthest sampling在生成的$\mathcal{Q}$中取出M个点作为种子，之后以这些种子为园心，以$r_d$为半径，将圆内的点聚合到一个M个子集$S_j , j=1 \dots M$中。这一圆按照测地距离进行划分，在进行这些操作之前，首先需要对整个模型进行归一化，令整个模型平铺之后的区域约为$\pi 1^2$，则每个子集中的点与所有点的百分比应大致为$\pi r^2_d / \pi 1^2 = r^2_d$，通过这一公式计算出一个子集中应有的点数，记为$\hat{n}$，则定义下述公式：

$$U_{imbalance}(S_j) = \frac{(|S_j| - \hat{n})^2}{\hat{n}}$$

但是，仅通过上述约束依然不够，在同一个子集中，仍然会有很多不同的点的分布，因此需要继续考虑在同一个子集中的点局部分布的情况。

在一个点的子集$S_j$中，我们去找到其中每一个点距离最近的邻居，对于子集中的第k个点，计算其距离为$d_{j,k}$，如果$S_j$内的点满足均匀分布，则每个点到它最近点的距离$\hat{d}$应该大致为$\sqrt{\frac{2\pi r_d^2}{|S_j|\sqrt{3}}}$，这一公式假设$S_j$所代表的子集为平面且每个点代表一个六边形，如下图所示：

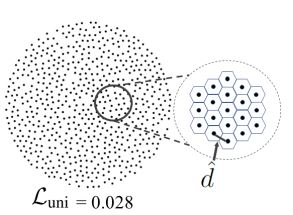
因此定义下述公式：

$$U_{clutter}(S_j) = \sum_{k=1}^{|S_j|}\frac{(d_{j,k}-\hat{d})^2}{\hat{d}}$$

因此，得到最终的Uniform loss为：

$$\mathcal{L}_{uni} = \sum_{j=1}^{M}U_{imbalance}(S_j)\cdot U_{clutter}(S_j)$$

Reconstruction loss

上述两种loss函数其实并没有限制点云是否覆盖在目标模型的表面上，因此需要继续引入reconstruction loss：

$$\mathcal{L}_{rec} = \min_{\phi : \mathcal{Q} \to \hat{\mathcal{Q}}} \sum_{q_i \in \mathcal{Q}} ||q_i - \phi (q_i)||_2$$

其中$\phi : \mathcal{Q} \to \hat{\mathcal{Q}}$是双射映射。

Compound loss

总的来看，我们通过最小化$\mathcal{L}_{G}$以及$\mathcal{L}_{D}$来训练PU-GAN:

$$\mathcal{L}_G = \lambda_{gan}\mathcal{L}_{gan}(G) + \lambda_{rec}\mathcal{L}_{rec} + \lambda_{uni}\mathcal{L}_{uni}$$

$$\mathcal{L}_D = \mathcal{L}_{gan}(D)$$