参考论文

FoldingNet: Point Cloud Auto-Encoder via Deep Grid Deformation

论文链接

Introduction

三维点云集合是一种不规则，无序的数据结构，很难通过二维神经网络的方法对其进行处理，之前对于点云的处理通常是将其体素化后再进行处理。

在本文中，作者将三维点云看作一个物体表面经过采样之后的结果，因此，一个三维的点云可以用二维网格点通过fold的操作（包括裁剪、折叠以及拉伸等）来获得。本文所提出的网络中decoder的部分，就模拟了折叠这一过程，从论文的实验结果就可以看到，只要经过两次折叠，就能够得到较好的生成模型，如下图所示：

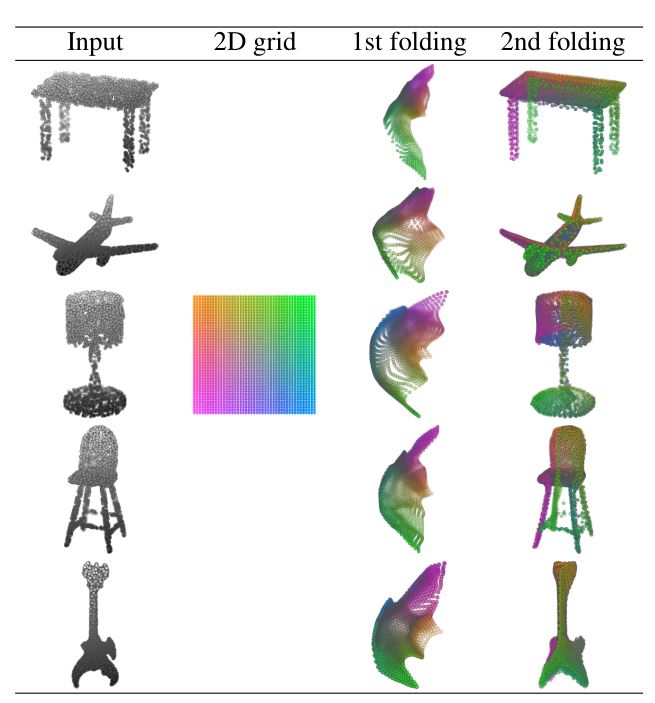
two-step-folding decoding

总结来看，这篇文章提出了一种新的端到端的自动编码器，能够直接处理无序的三维点云集合；提出了一种新的decoder的思路，通过折叠的方式重建三维模型；通过FoldingNet生成的codeword同其他方法相比，有着更好地分类效果。

The overview of FoldingNet

FoldingNet的网络结构如下图所示：

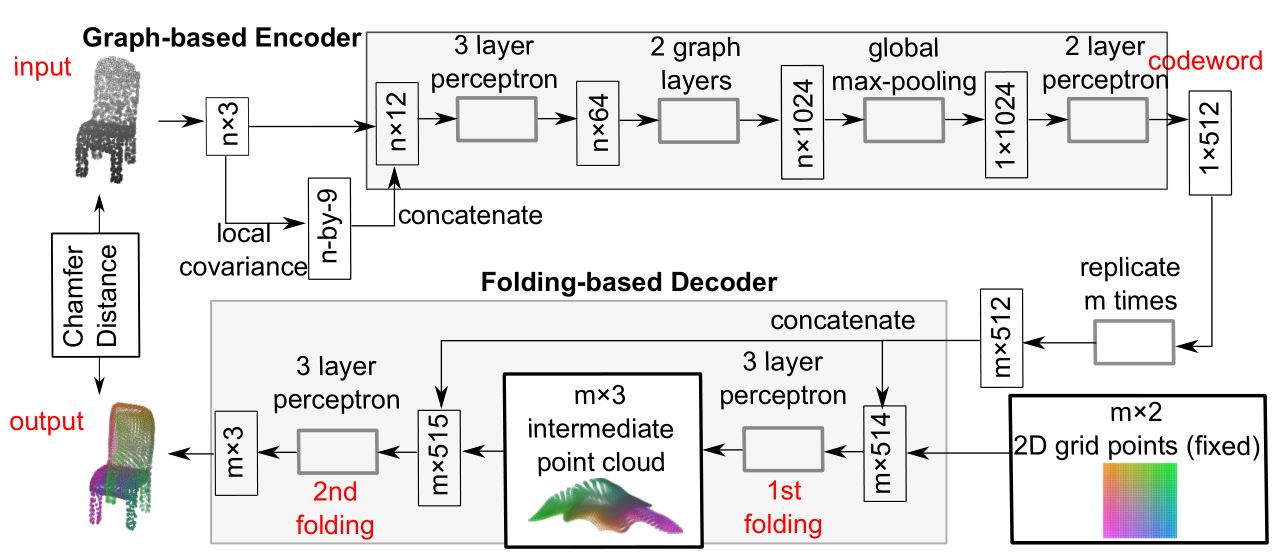
FoldingNet

Graph-based Encoder Architecture

对于encoder，需要提取出三维模型的特征信息，首先通过graph layer以及最大池化操作，将每个point临近的特征信息聚合起来，之后再连接一个2层感知器，最终得到一个512维的codeword。对于graph layer的设计，本文基于论文Mining point cloud local structures by kernel correlation and graph pooling所提出的模型进行了改进。

Folding-based Decoder Architecture

解码器基于folding的操作进行设计，由编码器生成的512维向量复制m份，将含有m个点的二维网格点与codeword连接起来组成m*514维的矩阵作为decoder的输入，每一层folding的输出为m*3的矩阵，表示一个含有m个点的三维点云模型，之后再将这一点云模型与codeword相连接，作为下一层folding的输入。

Loss Function

FoldingNet的重建误差定义为：

dCH(S,S^)=max{1∣S∣∑x∈Smin⁡x^∈S^∣∣x−x^∣∣2,1∣S^∣∑x^∈S^min⁡x∈S∣∣x^−x∣∣2}d_{CH}(S, \hat{S}) = max\{\frac{1}{|S|}\sum_{x \in S} \min_{\hat{x} \in \hat{S}}||x - \hat{x}||_2, \frac{1}{|\hat{S}|}\sum_{\hat{x} \in \hat{S}} \min_{x \in S}|| \hat{x} - x ||_2\}

其中，SS表示输入点集，S^\hat{S}表示重建模型的点集，loss function表示从SS到S^\hat{S}的距离与从S^\hat{S}到SS的距离必须同时小。